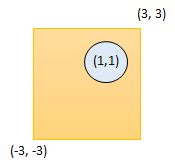给你一个以 (radius, x_center, y_center) 表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2)，其中 (x1, y1) 是矩形左下角的坐标，(x2, y2) 是右上角的坐标。

如果圆和矩形有重叠的部分，请你返回 True ，否则返回 False 。

换句话说，请你检测是否 存在 点 (xi, yi) ，它既在圆上也在矩形上（两者都包括点落在边界上的情况）。

示例 1：

img
img
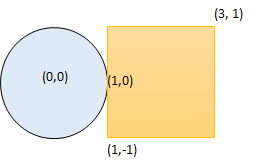
输入：radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出：true
解释：圆和矩形有公共点 (1,0)

示例 2：

img

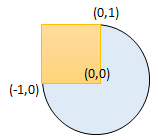
输入：radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出：true

示例 3：

img

输入：radius = 1, x_center = 1, y_center = 1, x1 = -3, y1 = -3, x2 = 3, y2 = 3
输出：true

示例 4：

输入：radius = 1, x_center = 1, y_center = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出：false

提示：

  • 1 <= radius <= 2000
  • -10^4 <= x_center, y_center, x1, y1, x2, y2 <= 10^4
  • x1 < x2
  • y1 < y2

思路

具体的做法参考知乎上的这篇回答。

class Solution {
    public boolean checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {

        // https://www.zhihu.com/question/24251545

        double recX = (x1 + x2) / 2.0d;
        double recY = (y1 + y2) / 2.0d;
        double[] u = new double[2];
        double[] v = new double[2];
        double[] w = new double[2];
        w[0] = Math.abs(xCenter - recX);
        w[1] = Math.abs(yCenter - recY);

        u[0] = (x2 - x1) / 2.0d;
        u[1] = (y2 - y1) / 2.0d;

        v[0] = w[0] - u[0];
        v[1] = w[1] - u[1];
        if (v[0] < 0) v[0] = 0;
        if (v[1] < 0) v[1] = 0;

        return Math.sqrt(v[0] * v[0] + v[1] * v[1]) <= radius;

    }
}

复杂度

常数级。