「论文笔记」Time Series is a Special Sequence: Forecasting with Sample Convolution and Interaction.
1. 概要
论文针对的是时序预测问题(Time Series Forecasting,TSF),根据时间序列的特点创新性地提出了一个多层的神经网络框架sample convolution and interaction network(SCINet)用于时序预测。模型在多个数据集上都展示了其准确率上的优越性,且时间成本相对其他模型(如时序卷积网络TCN)也更低。本篇论文工作包含以下几点:
- 说明了TCN不适合解决TSF问题,尤其是其中的因果卷积对模型准确率反而有负面影响
- 基于时间序列的独特性提出了一个多层TSF框架SCINet,通过计算permutation entropy(PE)可以证明新的模型有更强的预测能力
- 构造了SCINet的基本块SCI-Block,它将输入的数据/特征下采样为两个子序列,然后使用不同的卷积滤波器提取每个子序列特征以保留不同特征的信息。同时为了减少下采样过程中信息丢失造成的影响,在每个SCI-Block中加入了两个序列间卷积特征的学习。
2. 知识梳理
2.1. 相关模型
目前用于时间序列预测的主要有三类深度神经网络:
- RNNs及其变种(如LSTMs和GRUs)
- Transformer及其变种(如Reformer和Informer)
- TCNs
目前来看,TCN模型效果更好,并且可以与GNNs进行结合解决TSF(Time series forecasting)问题。
2.1.1. TCN-时序卷积网络
TCN这一网络结构起源于An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling这一论文,TCN在时间和效果上都普遍优于RNN,因此引起了巨大反响。
TCN中涉及到了最简单的CNN和RNN,除此之外还涉及到了扩张/空洞卷积(Dilated Convolution),因果卷积(Causal Convolution),残差卷积的跳层连接(Residual Connections)
- 因果卷积。要求对时刻
的预测 只能通过 时刻之前的输入 到 来判别,有一点类似于马尔科夫链。 - 膨胀卷积。对于普通的一维卷积操作,为了在输出侧获取足够的“感受野”,网络的层数需要跟追溯的历史信息长度成线性关系。为了降低网络复杂度,减少网络层数,TCN在卷积里注入空洞来增加感受野,可以将网络的层数下降到跟追溯的历史信息长度成指数关系
- 残差卷积的跳层连接。也称为残差卷积的跳层连接,在每层特征图中添加上一层的特征信息,使网络更深,加快反馈与收敛。
下图是TCN的整体网络结构:图(a)展示了空洞系数

TCNs具有两个原则
- 输入输出长度相等。
时刻后的数据不可以泄露到 时刻前。
但TSF问题并不需要满足以上两个原则,并且时间序列本身是一个非常特殊的序列数据,不应该使用针对普通序列的TCN模型一概而论。
2.1.2. Informer
2017年基于自注意力机制的Transformer架构横空出世,Google展示了它在机器翻译领域的绝佳性能。自此以后,无数文章前仆后继把Transformer用于各种序列信息建模,把所有之前用到RNN的问题都洗了几遍,把SOTA性能刷的也是死去活来。Tranformer确实在序列建模方面性能出色,但也有个重大弱点,那就是复杂度非常高,对计算和存储资源的消耗极大,速度也比较慢。因此近年来有很多工作尝试在对性能影响不大的前提下降低复杂度,Informer就是这样一个工作。
Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. 这一论文是AAAI 2021的Best Paper(但是在实际测试中,部分数据集上的表现非常糟糕)。Informer主要是对于Transformer模型的一个改进,Transformer结构有几个问题需要解决:
- self-attention的时间和空间复杂度都是
, 为序列长度。 - encoder-decoder结构在解码时step-by-step,预测序列越长,预测时间也就越长。
针对上面两个问题,Informer在Transformer基础上提出了三点改进:
- 提出了Prob Sparse Self-attention机制,时间复杂度降为
。 - 提出了Self-attention蒸馏机制来缩短每一层的输入序列长度,序列长度变短计算量和存储量自然也会下降
- 提出了生成式的decoder机制,在预测序列时一步得到结果,而不是step-by-step,直接将预测时间复杂度由
降到了 。
2.2. 知识整理
2.2.1. PE(排列熵)
Permutation Entropy(PE)是度量时间序列复杂性的一种方法,直观地来说,时间序列复杂性越低,序列的可预测性就越强,SCINet可以将时间序列的PE值降低,从而使序列“更容易预测”,其计算过程如下。
设有一维时间序列
对每行
统计每一行的下标顺序出现的次数除以
计算时间序列所有行的信息熵求和即为排列熵。
2.2.2. Multi-resolution analysis(多分辨率分析)
这是信号分析中的一个传统方法,并被应用到了时间序列分类问题中。
大概浏览了一下Multi-Scale Convolutional Neural Networks for Time Series Classification这篇论文(下图为模型),我理解这样一种方法就是类似于不断降采样,投入模型训练的过程,可能是不断二分,也可能是简单地进行一次二分就投入模型,总之是不同“分辨率”下对数据的处理训练。
2.2.3. Intermediate Supervision(中继监督)
中继监督也称为深度监督(deep supervision),其目的是为了浅层能够得到更加充分的训练,避免梯度消失和收敛速度过慢。
中继监督最早在2014年的Deeply-Supervised Nets论文中提出,但DSN的一个缺点在于使用的网络结构不够深,且辅助的分类器为传统的SVM模型。
2015年Training Deeper Convolutional Networks with Deep Supervision论文尝试了在更深层结构的网络中使用中继监督。这篇论文中给出了一个带有中继监督的8层深度卷积网络结构, 可以看到,图中在第四个卷积块之后添加了一个监督分类器作为分支。Conv4输出的特征图除了随着主网络进入Conv5之外,也作为输入进入了分支分类器。
后续中继监督作为一个优化模型训练的手段被广泛应用于各种深度学习网络中,如ECCV2016的Stacked Hourglass Networks,本论文中给出的Trellis networks for sequence modeling等等。
3. SCINet: Sample Convolution and Interaction Networks

SCINet的整体结构如上图所示
- 图(a)是基本块SCI-Block,将输入数据/特征进行下采样后输入两个分离的子序列中(
- 图(b)是一个SCINet,它使用了二叉树将SCI-Block组合起来,在经过了所有SCI-Block中的操作后,在Concat & Realign层将信息组合并添加到原始时间序列进行预测。
- 图(c)展示了SCINet堆叠起来形成的更大的网络Stacked SCINet,这样的网络可以用来预测更复杂的时间序列。
3.1. SCI-Block
这一部分将时间序列分为

SCI块的结构如上图所示。
使用两个不同的一维卷积模块
使用两个不同的一维模块
其中,
3.2. SCINet
整个SCINet的结构是一个二叉树,在每个SCI-Block中时间序列被分为两个部分,随着二叉树深度的增加,时间序列的“时间分辨率”不断降低,更精细的时序信息也会被提取出来,通过这样的方式,TSF序列中短期和长期的依赖关系都会被提取出来。
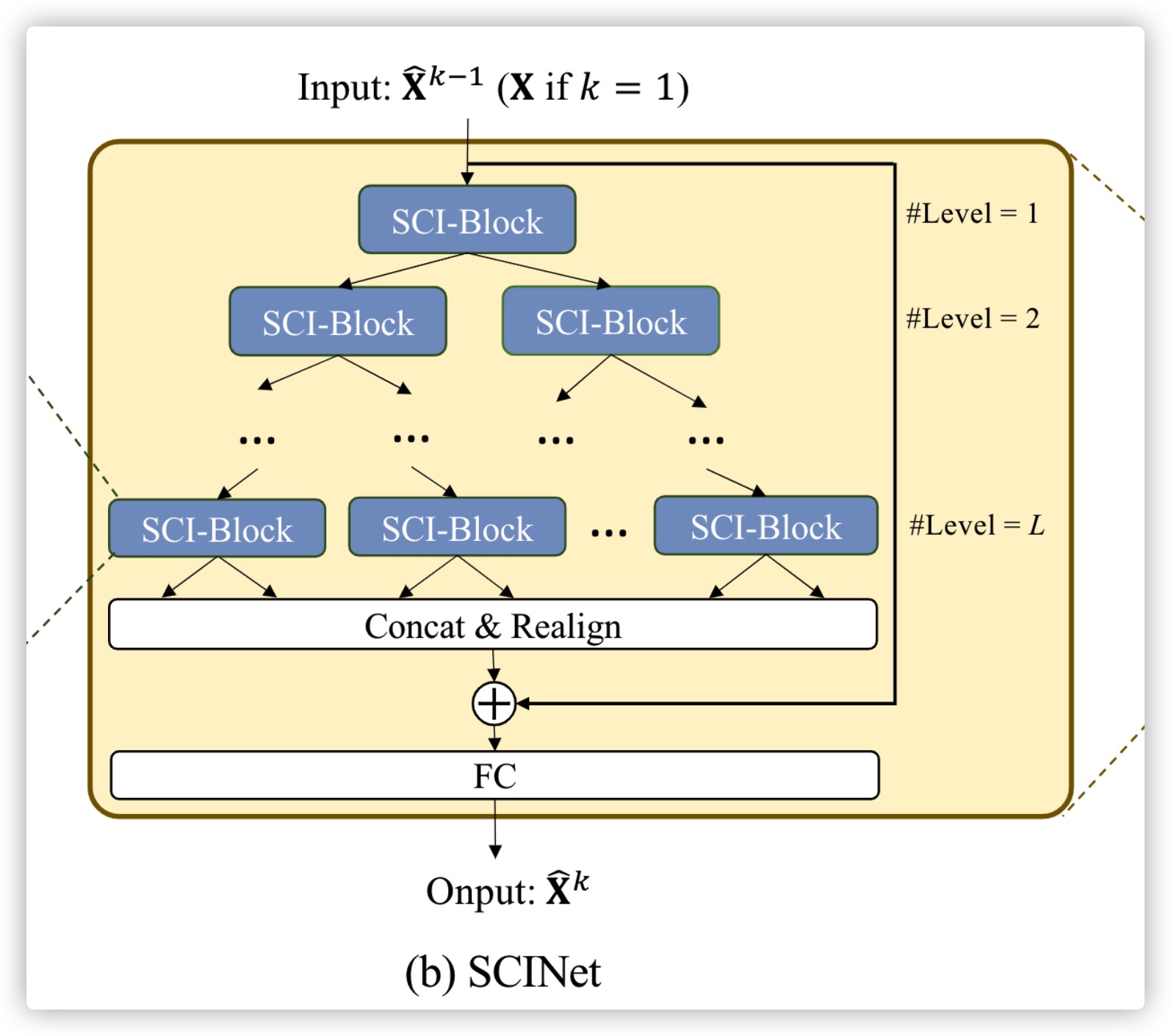
在经过
最后进行全连接层,得出预测结果或特征(根据SCINet在Stacked SCINet所处的层次)(这里也保证了输入与输出的长度不一定一致)
SCINet相比TCN的时间成本大大降低,TCN所需的卷积操作数为
3.3. 使用中继监督的Stacked SCINet
在每个SCINet的输出处使用了中继监督(使用ground-truth进行计算,见下个部分“损失函数”),第k层的输出
3.4. 损失函数
一个具有
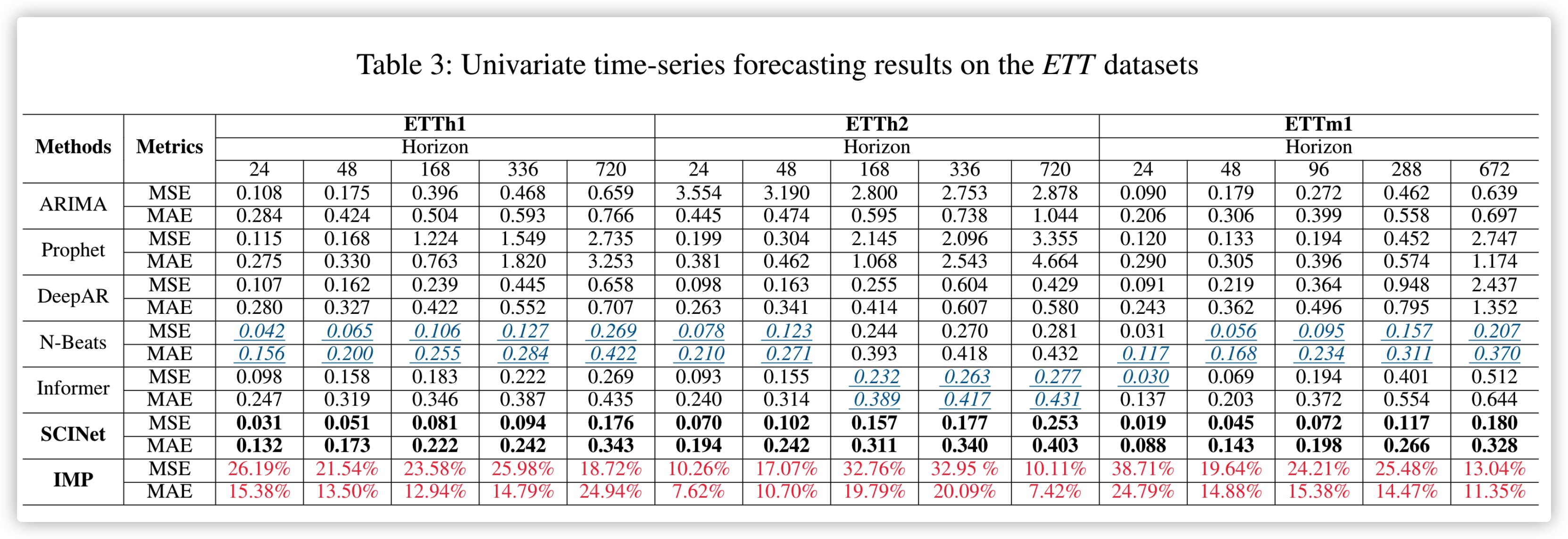
4. 实验结果
其中对于单步预测的评估使用的是最后一次的预测值,对于多步预测的评估使用的是平均值。
EET数据集上的表现如图所示,可以看出SCINet>TCNs>Transformer>RNNs。

上图为多变量实验数据。
上图为单变量实验数据。

在PeMS这种时空数据集上,SCINet可以在没有复杂的空间依赖模型的情况下仍取得很好的效果。

论文进一步利用排列熵(PE)来对比原始输入和SCINet学习的增强表示的可预测性。PE值较低的时间序列理论上更容易预测。从下图可以观察到,与原始输入相比,SCINet学习的增强表示具有较低的PE值。
5. 局限
该网络只考虑了对时间序列建模,并没有考虑到数据在空间上的关系,作者认为未来可以在这个方向上进行改进。